Cho A là 1 ma trận. Ma trận có được từ A bằng phương pháp xóa đi 1 số dòng và 1 số cột được gọi là ma trận con của A. Định thức của ma trận con cấp okay của A được gọi là định thức con cấp okay của A.
Hạng của ma trận A là r ví dụ:
A có 1 định thức con cấp r khác 0 và mọi định thức con cấp s (s > r) đều bằng 0.
Ta thường ký hiệu của ma trận A là R(A)
Thí dụ: Cho ma trận (A = left( start{array}{l} 1,,,,,1,,,,1 0,,,,1,,,,1 0,,,,0,,,1 finish{array} proper)). Tìm hạng của A
Vì (left| A proper| = 1 ne 0) nê R(A)=3
Thí dụ: Cho ma trận (A = left( start{array}{l} 1,,,,,2,,,,3 4,,,,5,,,,6 7,,,,8,,,9 finish{array} proper)). Tìm hạng của A
Vì (left| A proper| = 0,và,left| start{array}{l} 1,,,,,2 4,,,,5 finish{array} proper| = – 3 ne 0)nên R(A)=2
1 số hệ quả:
(start{array}{l} R({A_{m,x,n}}) le ,min left{ {m,n} proper} R(A) = R({A^T}) R({A_{n,x,n}}) = n Leftrightarrow left| {{A_{m,x,n}}} proper| ne 0 finish{array})
Xét ma trận A. Ta có:
R(A) = hạng của hệ vectơ dòng của A = hạng của hệ vectơ cột của A.
- 1 dòng của ma trận A gọi là dòng tầm thường ví dụ gồm toàn số 0.
- Phần tử khác 0 trước tiên tính từ trái sang cần của 1 dòng ko tầm thường được gọi là phần tử dẫn đầu.
- 1 dòng ko tầm thường gọi là có bậc okay ví dụ phần từ dẫn đầu là phần tử thứ okay tính từ trái sang cần.
Thí dụ: Xét ma trận (A = left( start{array}{l} 2,,,,,,0,,,,,1,,,,,0 0,, – 3,,,,,0,,,,2 1,,,,,2,, – 3,,,,1 0,,,,,0,,,,,0,,,,,,,0 finish{array} proper))
Ta có:
Dòng thứ 1 là dòng ko tầm thường bậc 1.
Dòng thứ 2 là dòng ko tầm thường bậc 2.
Dòng thứ 3 là dòng ko tầm thường bậc 1.
Dòng thứ 4 là dòng tầm thường.
1 ma trận A có dạng bậc thang ví dụ:
- Những dòng tầm thường (ví dụ có) trên dưới đáy.
- Những dòng ko tầm thường có bậc nâng cao thực sự.
Thí dụ: (A = left( start{array}{l} 2,,,,,,0,,,,,1,,,,,0 0,, – 3,,,,,0,,,,2 0,,,,,0,,,,,,0,,,,0 finish{array} proper)) là 1 ma trận bậc thang
1 ma trận bậc thang thu gọn là 1 ma trận bậc thang có thêm những tính chất:
- Những phần tử dẫn đầu (gọi là phần tử trụ) đều là số 1
- Những phần tử trên trên và cùng cột sở hữu phần tử trụ đều là số 0.
Thí dụ: (A = left( start{array}{l} 1,,,,,,0,,,,,3,,,,,0,,,,,4 0,,,,,,1,,,,,2,,,,0,, – 1 0,,,,,0,,,,,,0,,,,1,,,,,2 finish{array} proper))là 1 ma trận bậc thang thu gọn
Cho A là 1 ma trận bậc thang. Lúc ấy, từ định nghĩa hạng cùa ma trận, ta dễ thấy: R(A) = số dòng ko tầm thường của ma trận A
Thí dụ: Xét (A = left( start{array}{l} 1,,,,,,2,,,,,3,,,,,4 0,,,,,2,,,,,0,,,,,4 0,,,,,0,,,,,,0,,,,0 finish{array} proper)). Vì A có dạng bậc thang và có 2 dòng ko tầm thường nên R(A)=2.
Những phép biến đổi sau đây trên ma trận được gọi là những phép biến đổi sơ cấp trên dòng
- Đổi chỗ 2 dòng.
- Nhân 1 dòng sở hữu 1 số khác 0.
- Cùng vào 1 dòng bởi bội của 1 dòng khác.
Dùng những phép biến đổi sơ cấp trên dòng, ta có thể đưa 1 ma trận vê dạng bậc thang hay dạng bậc thang thu gọn.
Ta có thuật toán đưa 1 ma trận về dạng bậc thang như sau :
- Bước 1: Tìm cột ko tầm thường trước tiên tính từ trái sang cần. Giả sử cột ấy là cột j .
- Bước 2: Đổi chỗ những dòng sao cho 1 phần tử khác 0 của cột j đứng vào dòng 1, nghĩa là ({a_{{rm{ij}}}} ne 0).
- Bước 3 : dùng ({a_{{rm{ij}}}} ne 0) khiến phần tử trụ, đưa những số khác 0 cùng cột và đứng dưới ({a_{{rm{1j}}}}) về 0 bằng những phép biến đổi sơ cấp ({a_{{rm{1j}}}} d_i-{a_{{rm{ij}}}} d_1) (nhân dòng i sở hữu ({a_{{rm{1j}}}} ) , nhân dòng 1 sở hữu (-{a_{{rm{ij}}}} ) cùng lại và viết vào dòng i).
- Bước 4 : Lặp lại những bước trên sở hữu ma trận con có từ ma trận đầu bằng phương pháp bỏ dòng 1.
- Bước 5 : Lặp lại những bước trên cho tới lúc có được dạng bậc thang.
Thí dụ Đưa ma trận sau đây về dạng bậc thang
(A = left( start{array}{l} 1,,,,,2,,, – 3,,,0 2,,,4,,, – 2,,,2 3,,,6,,, – 4,,,3 finish{array} proper))
Giải
Ta có:
dạng bậc thang
Ta có thuật toán đưa 1 ma trận bậc thang về dạng bậc thang thu gọn như sau:
Cho (A=({a_{{rm{ij}}}} )) là ma trận có dạng bậc thang sở hữu những phần tử dẫn đầu lần lươt là ({a_{{rm{1j_1}}}} ,{a_{{rm{2j_2}}}},…,{a_{{rm{rj_r}}}}) .
Bước 1: Nhân dòng r sở hữu (frac{một}}{{{a_{{rm{r}}{{rm{j}}_{rm{r}}}}}}}) để có phần tử dẫn đầu của dòng r là 1.
Bước 2 : Dùng phần tử ({a_{{rm{r}}{{rm{j}}_{rm{r}}}}}=1) như là phần tử trụ, đưa những phần tử cùng cột và trên trên a về số 0 bằng phép biến đôi sơ cấp (d_i-{a_{{rm{r}}{{rm{j}}_{rm{r}}}}}d_r).
Bước 3 : Lặp lại những bước trên đối sở hữu những dòng r-1, r-2,…,2.
Bước 4 : Nhân dòng 1 sở hữu (frac{một}}{{{a_{{rm{một}}}{{rm{j}}_{rm{một}}}}}}}}).
Để đưa về dạng bậc thang thu gọn, ta có thể ứng dụng 2 thuật toán nêu trên, đưa ma trận về dạng bậc thang rồi đưa về dạng bậc thang thu gọn. Bên cạnh ra, ta có thể ứng dụng thuật toán đưa ma trận về dạng bậc thang có sửa đổi 1 chút:
Tại bước 3, thay đổi vì chỉ đưa những số khác 0 đứng dưới và cùng cột sở hữu phân tử dẫn đầu về số 0, thì ta đưa cả những số khác 0 đứng trên và cùng cột sở hữu phần tử dẫn đầu về số 0.
Cuối cùng, lúc đã có được dạng bậc thang, ta chia những dòng tầm thường cho phần tử dẫn đầu của chúng để đưa những phần tử dẫn đầu về số 1.
Thí dụ: Đưa ma trận sau đây về dạng bậc thang thu gọn
(A = left( start{array}{l} 2,,,,,1,,,,,,5,,,,,,3 1,, – 4,,,,,2,,,,,3 3,,,,,,0,,,,,1,,,,,,2 finish{array} proper))
Giải
Ta có
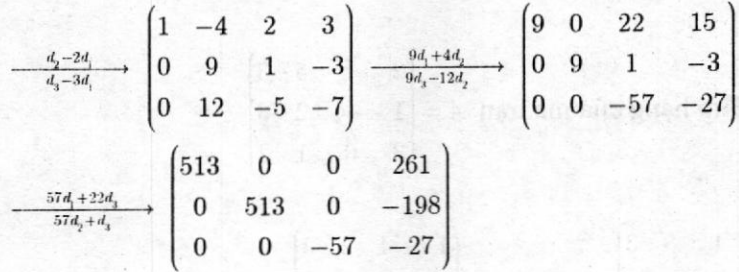
dạng bậc than thu gọn.
Những phép biến đổi sơ cấp trên dòng của 1 ma trận ko khiến thay đổi đổi hạng của ma trận..
Thí dụ: Tìm hạng của ma trận (A = left( start{array}{l} 1,,,,,2,,,,, – 3,,,,,,0 2,,,,4,,,,, – 2,,,,,,2 3,,,,6,,,,, – 4,,,,,,3 finish{array} proper))
Ta có:
Vì R(B) = 2 nên R(A) = 2.
Ứng dụng:
Để đánh giá tính độc lập tuyến tính, phụ thuộc tuyến tính của 1 hệ n vectơ, ta có thể sắp những vectơ đấy thành những dòng của 1 ma trận A, rồi tìm hạng của A. Trường hợp R(A) = n thì hệ ấy là 1 hệ độc lập tuyến tính, ví dụ R(A) < n thì hệ ấy là 1 hệ phụ thuộc tuyến tính.
Thí dụ: Xét tính độc lập tuyến tính, phụ thuộc tuyến tính của hệ vectơ sau đây: V = {(1,2,0,3), (2,1,-4,0), (-2,0,1,1)}
Giải
Ta lập ma trận
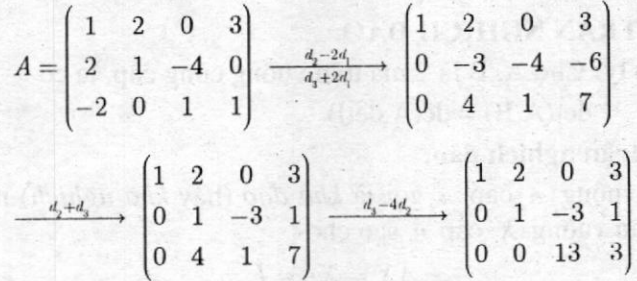
Suy ra: R(A) = 3. Vậy, V độc lập tuyến tính.
Để tìm 1 cơ sở và số chiều của ko gian vectơ con sinh bởi 1 hệ vectơ, ta lập ma trận A gồm những dòng là những vectơ ấy, rồi đưa A về dạng bậc thang. Những dòng ko tầm thường của A tạo thành 1 cơ sở của ko gian vectơ con sinh bởi hệ vectơ ấy, và số dòng ko tâm thường cao nhất} của A trên dạng bậc thang là số chiều của ko gian sinh.
Thí dụ: Tìm 1 cơ sở và số chiều của ko gian (leftlangle V rightrangle ) sở hữu V = {(1,-2,5,4), (2,-2,1,0), (3,4,0,2)}
Giải: Ta lập ma trận
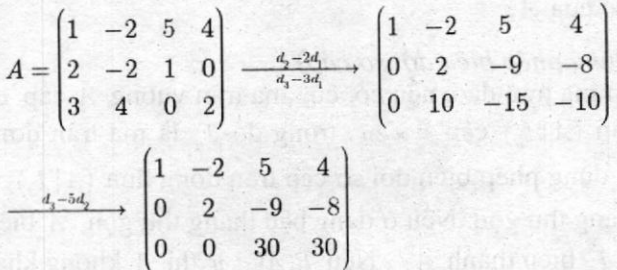
Suy ra: R(A) = 3, nên (dim leftlangle V rightrangle =3)
Và 1 cơ sở của (leftlangle V rightrangle )là {(1;-2;5;4),(0;2;-9;-8).(0;0;1;1)} .
